Binary Tree Basics
Table of Contents
1. Basics of Binary Search Trees
Each node has a maximum of two children. The value of the left child is less than the node's value. The value of the right child is greater than or equal to the node's value.
A node has a value, and pointers to right and left children.
from dataclasses import dataclass
@dataclass
class Node:
value: int
left: 'Node' = None
right: 'Node' = None
1.1. Building a BST
A tree can be represented as an object with a pointer to the root node. An insert method can be used to insert nodes to the correct position maintaining the expected order by value.
@dataclass
class BST:
root: 'Node' = None
def insert(self, value):
if self.root is None:
self.root = Node(value)
else:
self._insert_into_tree(self.root, value)
def _insert_into_tree(self, node, value):
if value < node.value:
if node.left is None:
node.left = Node(value)
else:
self._insert_into_tree(node.left, value)
else:
if node.right is None:
node.right = Node(value)
else:
self._insert_into_tree(node.right, value)
We can then build a tree.
items = [7, 9, 5, 2, 7, 8, 10, 5]
tree = BST()
for i in items:
tree.insert(i)
print(tree)
BST(root=Node(value=7, left=Node(value=5, left=Node(value=2, left=None, right=None), right=Node(value=5, left=None, right=None)), right=Node(value=9, left=Node(value=7, left=None, right=Node(value=8, left=None, right=None)), right=Node(value=10, left=None, right=None))))
At this point, the tree looks like below:
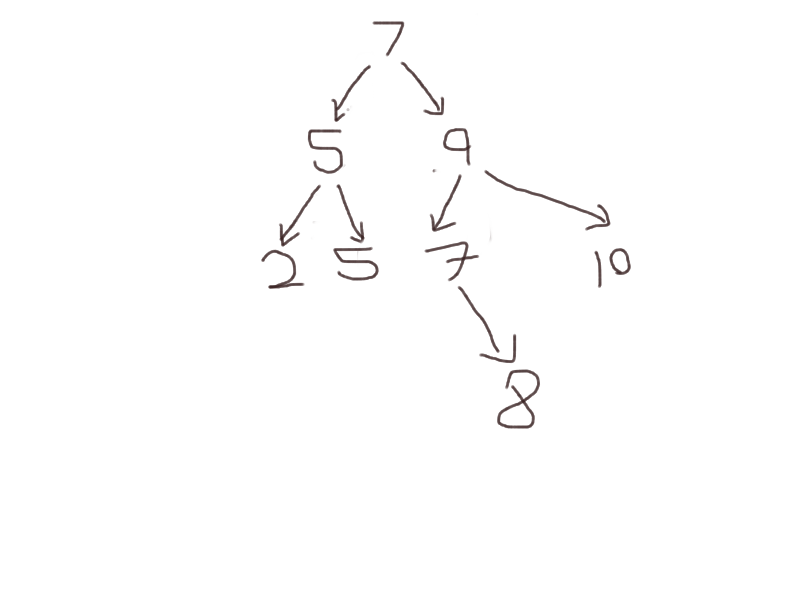
1.2. In order Traversal
For each node, the action is performed on the values in the left subtree, then the current node's value, then the value of the right subtree.
This can be used to perform an action in ascending order of values in the tree.
Here, the action would be to simply print out the node's value.
def action(value):
print(value, end=" ")
1.2.1. Recursive
The traversing function is called recursively on each node
def inorder_recursive(node, action):
if node.left:
inorder_recursive(node.left, action)
action(node.value)
if node.right:
inorder_recursive(node.right, action)
inorder_recursive(tree.root, action)
2 5 5 7 7 8 9 10
1.2.2. Iterative
Traversing iteratively uses a stack to track nodes to visit. We ensure that the nodes action is performed on the nodes in the correct order by inserting the nodes into the stack in reverse order.
Additionally, we keep track of nodes have been processed, i.e. their children inserted into the stack, to avoid getting stack in an infinite loop.
def inorder_iterative(node, action):
stack = []
processed = set()
stack.append(node)
while stack:
n = stack.pop()
if id(n) in processed:
action(n.value)
else:
if n.right:
stack.append(n.right)
stack.append(n)
if n.left:
stack.append(n.left)
processed.add(id(n))
inorder_iterative(tree.root, action)
2 5 5 7 7 8 9 10
1.3. Pre-Order Traversal
For each node, the action is performed in the node's value, followed by the node's left subtree values then the node's right subtree values.
This can be used, for instance, to create a copy of the tree with the same structure since each parent node is visited before the children.
1.3.1. Recursive
def preorder_recursive(node, action):
action(node.value)
if node.left:
preorder_recursive(node.left, action)
if node.right:
preorder_recursive(node.right, action)
preorder_recursive(tree.root, action)
7 5 2 5 9 7 8 10
1.3.2. Iterative
A stack is used to keep track of nodes to traverse. Action is performed in order of popping items from the stack
def preorder_iterative(node, action):
stack = []
stack.append(node)
while stack:
n = stack.pop()
if n.right:
stack.append(n.right)
if n.left:
stack.append(n.left)
action(n.value)
preorder_iterative(tree.root, action)
7 5 2 5 9 7 8 10
1.4. Post-Order Traversal
For each node, the action is performed on the left subtree values, then the right subtree values and finally the current node's values.
This can be used, for instance, to delete a tree, because each nodes children are processed before the node itself, all the way to the root.
1.4.1. Recursive
def postorder_recursive(node, action):
if node.left:
postorder_recursive(node.left, action)
if node.right:
postorder_recursive(node.right, action)
action(node.value)
postorder_recursive(tree.root, action)
2 5 5 8 7 10 9 7
1.4.2. Iterative
def postorder_iterative(node, action):
stack = []
stack.append(node)
processed = set()
while stack:
n = stack.pop()
if id(n) in processed:
action(n.value)
else:
stack.append(n)
if n.right:
stack.append(n.right)
if n.left:
stack.append(n.left)
processed.add(id(n))
postorder_iterative(tree.root, action)
2 5 5 8 7 10 9 7
1.5. Breadth first search
The examples we've been looking at so far demonstrate some form of depth first search, when we select a route down the tree, we traverse all terminal nodes before backtracking to a different route.
With breath first search, however, we traverse all the nodes at a particular level of the tree before moving on to the lower level.
To implement this, we make use of a queue instead for its First In First out semantics. The goal is to queue each level's nodes in order from left to right and as we retrieve them, we start queueing the next level's nodes following the same order.
We use python's deque data structure which is short for 'double
ended queue'.
from collections import deque
def breadth_first(node, action):
queue = deque()
queue.append(node)
while queue:
n = queue.popleft()
action(n.value)
if n.left:
queue.append(n.left)
if n.right:
queue.append(n.right)
breadth_first(tree.root, action)
7 5 9 2 5 7 10 8
1.6. Deleting a node in a BST
To delete a node, we need to make sure that the BST property is
maintained i.e. left_child.value <= parent.value <= right_child.value.
To do this, once we identify the node to delete, we replace either with the smallest valued node it its right subtree, or the largest valued node in its left subtree.
To demonstrate delete, we'll extend the existing BST class with delete functionality.
class BST2(BST):
def delete(self, value):
self._delete(self.root, value)
def _delete(self, node, value):
if node is None:
pass
if value < node.value:
node.left = self._delete(node.left, value)
elif value > node.value:
node.right = self._delete(node.right, value)
else:
# Current node is to be deleted
# Consider 3 possibilities
# - no children
# - one child
# - two children
if not node.right and not node.left:
# no children
node = None
elif not node.right:
# has a left child, replace
node = node.left
elif not node.left:
# has a right child, replace
node = node.right
else:
# has two children
# two options, overwrite with smallest from right, or largest from left
replacement_value = self._get_smallest(node.right)
node.value = replacement_value
# delete node with replacement value
node.right = self._delete(node.right, replacement_value)
return node
def _get_smallest(self, node):
while node.left:
node = node.left
return node.value
Next, we create a new tree and test deletion
tree2 = BST2()
for i in items:
tree2.insert(i)
assert tree2.root.value == 7
assert tree2.root.right.left.right.value == 8
# delete root
tree2.delete(7)
# topmost 4 should have been replace by the other 7
assert tree2.root.value == 7
assert tree2.root.right.left.value == 8
# delete root
tree2.delete(7)
assert tree2.root.value == 8
assert tree2.root.right.left is None
tree2.delete(5)
# topmost 5 replaced by second one
assert tree2.root.left.value == 5
assert tree2.root.left.right is None
# delete terminal node 10
tree2.delete(10)
assert tree2.root.right.value == 9
assert tree2.root.right.right is None
tree2.delete(5)
# right terminal node should have 2
assert tree2.root.left.value == 2
assert tree2.root.left.right is None
